gpcfa-examples
Jinsong Chen
2022-05-15
Source:vignettes/Examples/gpcfa-examples.Rmd
gpcfa-examples.RmdNote: the estimation process can be time consuming depending on the computing power. You can same some time by reducing the length of the chains.
Categorical Data with Missingness but no Local Dependence:
- Load the package, obtain the data, and check the true loading pattern (qlam) and local dependence.
## LAWBL Package (version 1.5.0; 2022-05-13)
## For tutorials, see https://jinsong-chen.github.io/LAWBL/
dat <- sim18ccfa40$dat
dim(dat)## [1] 1000 18
summary(dat) #10% missingness at random## V1 V2 V3 V4 V5
## Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.00 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :2.000 Median :2.00 Median :2.000 Median :2.000 Median :2.000
## Mean :2.446 Mean :2.47 Mean :2.471 Mean :2.454 Mean :2.479
## 3rd Qu.:3.000 3rd Qu.:3.00 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.00 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :86 NA's :103 NA's :98 NA's :101 NA's :102
## V6 V7 V8 V9
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :2.000 Median :2.000 Median :3.000 Median :3.000
## Mean :2.459 Mean :2.472 Mean :2.538 Mean :2.499
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :105 NA's :99 NA's :94 NA's :99
## V10 V11 V12 V13
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :2.000 Median :2.000 Median :2.000 Median :3.000
## Mean :2.486 Mean :2.477 Mean :2.481 Mean :2.553
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :99 NA's :100 NA's :98 NA's :90
## V14 V15 V16 V17
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :2.000 Median :3.000 Median :2.500 Median :2.000
## Mean :2.478 Mean :2.529 Mean :2.511 Mean :2.475
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :84 NA's :107 NA's :100 NA's :107
## V18
## Min. :1.000
## 1st Qu.:2.000
## Median :2.000
## Mean :2.478
## 3rd Qu.:3.000
## Max. :4.000
## NA's :108
J <- ncol(dat) # no. of items
K <- 3 # no. of factors
sim18ccfa40$qlam## [,1] [,2] [,3]
## [1,] 0.7 0.0 0.0
## [2,] 0.7 0.0 0.0
## [3,] 0.7 0.0 0.0
## [4,] 0.7 0.0 0.0
## [5,] 0.7 0.3 0.0
## [6,] 0.7 0.3 0.0
## [7,] 0.0 0.7 0.0
## [8,] 0.0 0.7 0.0
## [9,] 0.0 0.7 0.0
## [10,] 0.0 0.7 0.0
## [11,] 0.0 0.7 0.3
## [12,] 0.0 0.7 0.3
## [13,] 0.0 0.0 0.7
## [14,] 0.0 0.0 0.7
## [15,] 0.0 0.0 0.7
## [16,] 0.0 0.0 0.7
## [17,] 0.3 0.0 0.7
## [18,] 0.3 0.0 0.7
sim18ccfa40$LD## row col- E-step: Estimate with the GPCFA-LI model (E-step) by setting LD=F and the design matrix Q. Only a few loadings need to be specified in Q (e.g., 2 per factor). Longer chain is suggested for more accurate and stable estimation.
Q<-matrix(-1,J,K); # -1 for unspecified items
Q[1:2,1]<-Q[7:8,2]<-Q[13:14,3]<-1 # 1 for specified items
Q## [,1] [,2] [,3]
## [1,] 1 -1 -1
## [2,] 1 -1 -1
## [3,] -1 -1 -1
## [4,] -1 -1 -1
## [5,] -1 -1 -1
## [6,] -1 -1 -1
## [7,] -1 1 -1
## [8,] -1 1 -1
## [9,] -1 -1 -1
## [10,] -1 -1 -1
## [11,] -1 -1 -1
## [12,] -1 -1 -1
## [13,] -1 -1 1
## [14,] -1 -1 1
## [15,] -1 -1 -1
## [16,] -1 -1 -1
## [17,] -1 -1 -1
## [18,] -1 -1 -1
m0 <- pcfa(dat = dat, Q = Q,LD = FALSE, cati = -1,burn = 5000, iter = 5000)
# summarize basic information
summary(m0)## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 9.888889
##
## $`LD Allowed`
## [1] FALSE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0542 1.2080
## [2,] 1.3675 2.1326
## [3,] 1.7886 3.4113
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 4092.631 3636.207 3268.126
##
## $Time
## user system elapsed
## 172.29 0.08 172.53
#summarize significant loadings in pattern/Q-matrix format
summary(m0, what = 'qlambda') ## 1 2 3
## I1 0.7494 0.0000 0.0000
## I2 0.7502 0.0000 0.0000
## I3 0.7564 0.0000 0.0000
## I4 0.7714 0.0000 0.0000
## I5 0.7668 0.2186 0.0000
## I6 0.7243 0.2176 0.0000
## I7 0.0000 0.7452 0.0000
## I8 0.0000 0.7423 0.0000
## I9 0.0000 0.7394 0.0000
## I10 0.0000 0.7101 0.0000
## I11 0.0000 0.7108 0.2506
## I12 0.0000 0.7043 0.2496
## I13 0.0000 0.0000 0.7405
## I14 0.0000 0.0000 0.7169
## I15 0.0000 0.0000 0.7262
## I16 0.0000 0.0000 0.7056
## I17 0.2992 0.0000 0.7270
## I18 0.3182 0.0000 0.6622
#factorial eigenvalue
summary(m0,what='eigen') ## est sd lower upper sig
## F1 3.7133 0.5313 2.6856 4.7797 1
## F2 3.4365 0.4868 2.5644 4.4104 1
## F3 3.3232 0.4754 2.4596 4.2694 1
#thresholds for categorical items
summary(m0,what='thd')## [,1] [,2] [,3]
## [1,] -1.3548 0.0686 1.6157
## [2,] -1.4361 0.0550 1.4945
## [3,] -1.4567 0.0561 1.5076
## [4,] -1.3796 0.0598 1.6020
## [5,] -1.4236 0.0158 1.4669
## [6,] -1.4962 0.0788 1.5805
## [7,] -1.4978 0.0360 1.6452
## [8,] -1.5220 -0.0578 1.4083
## [9,] -1.4744 -0.0130 1.5056
## [10,] -1.4871 0.0100 1.6224
## [11,] -1.4518 0.0191 1.5725
## [12,] -1.5360 0.0168 1.6319
## [13,] -1.5612 -0.0596 1.3936
## [14,] -1.4252 0.0421 1.5051
## [15,] -1.5544 -0.0322 1.4690
## [16,] -1.4710 -0.0154 1.3745
## [17,] -1.4405 0.0543 1.4854
## [18,] -1.5317 0.0301 1.5441
#plotting factorial eigenvalue
plot_lawbl(m0) # trace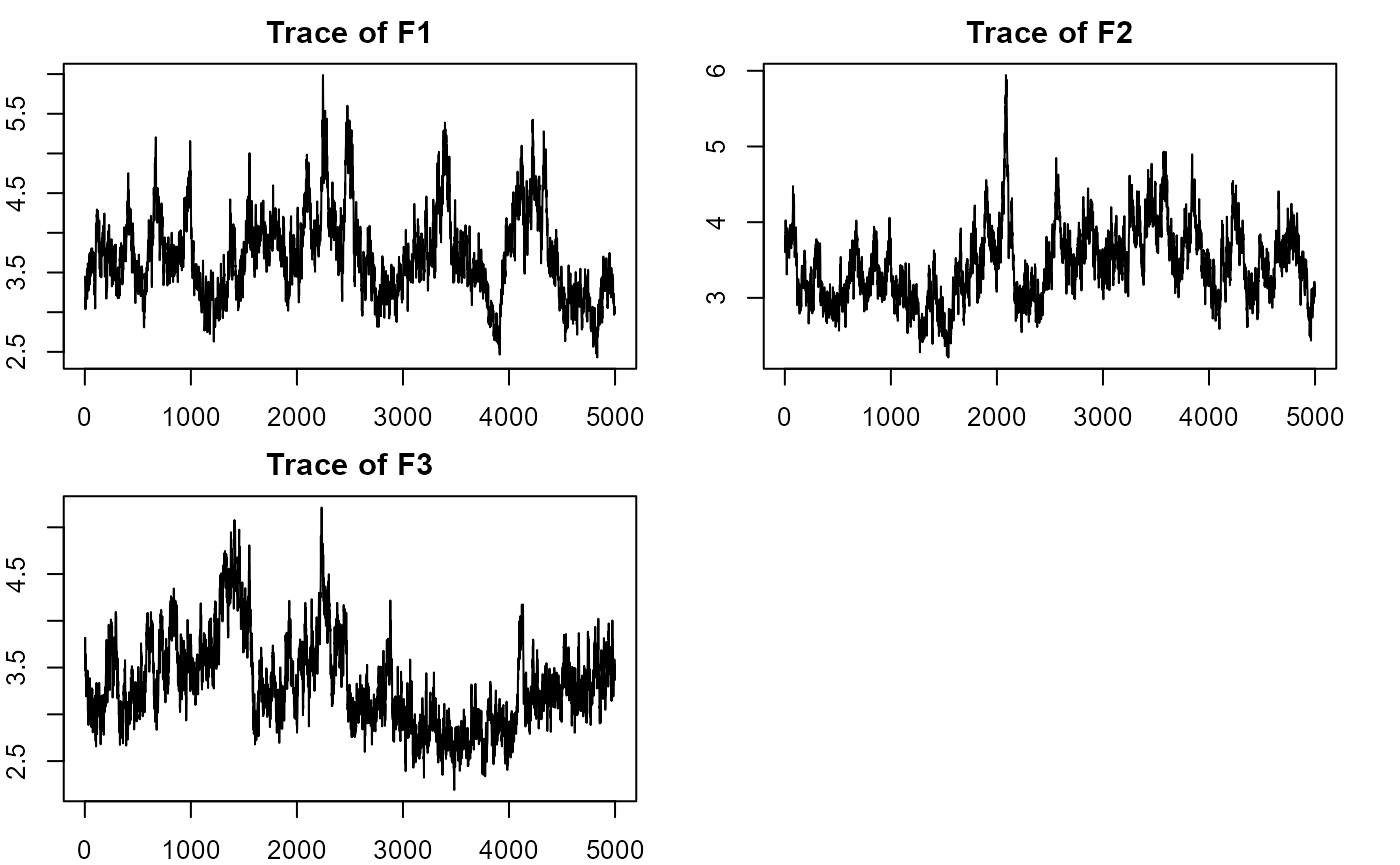
plot_lawbl(m0, what='density') #density
plot_lawbl(m0, what='EPSR') #EPSR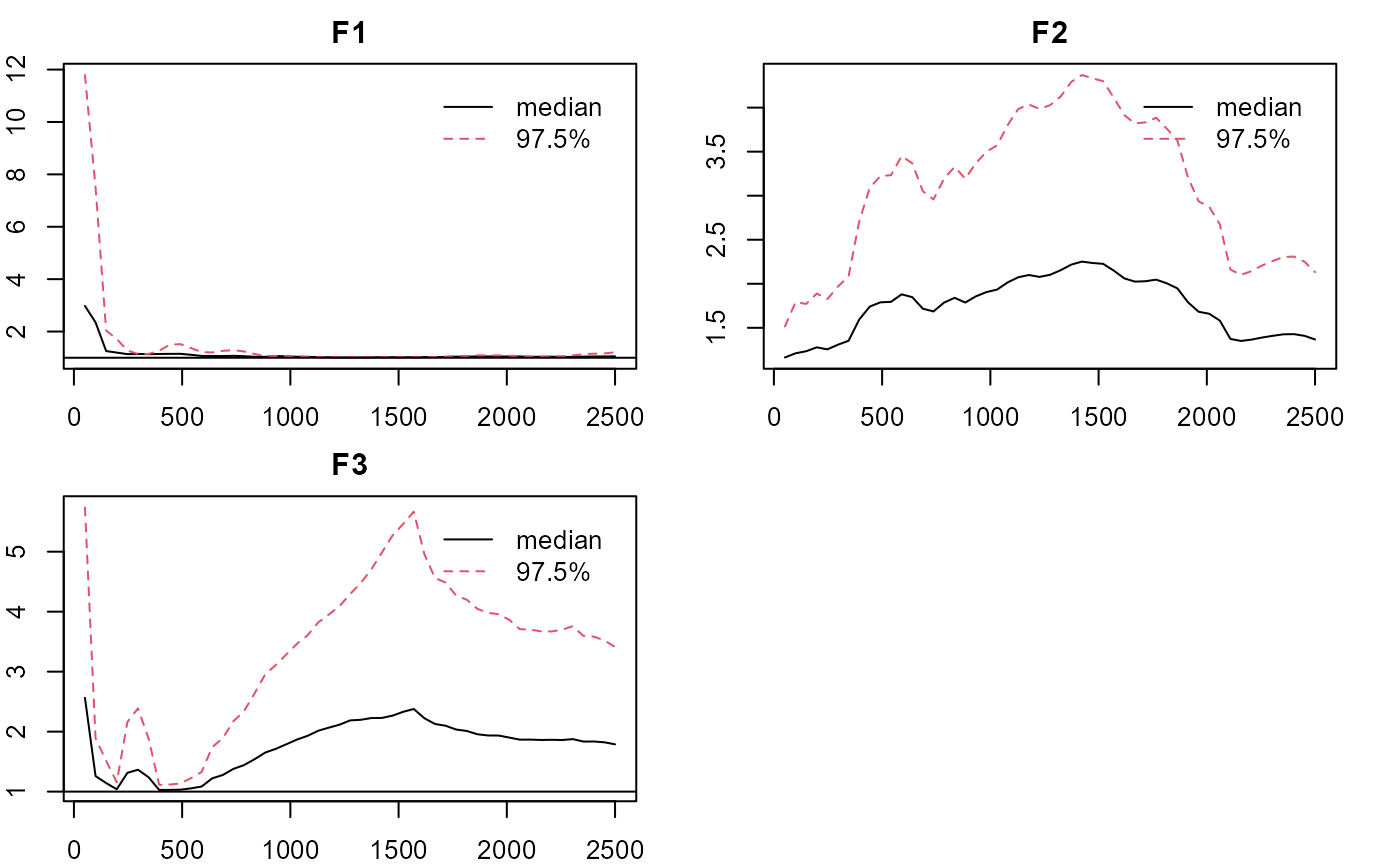
- C-step: Reconfigure the Q matrix for the C-step with one specified loading per item based on results from the E-step. Estimate with the GPCFA model by setting LD=TRUE (by default). Longer chain is suggested for more accurate and stable estimation.
Q<-matrix(-1,J,K);
tmp<-summary(m0, what="qlambda")
cind<-apply(tmp,1,which.max)
Q[cbind(c(1:J),cind)]<-1
#alternatively
#Q[1:6,1]<-Q[7:12,2]<-Q[13:18,3]<-1 # 1 for specified items
m1 <- pcfa(dat = dat, Q = Q, cati = -1)
summary(m1)## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 9.888889
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0368 1.1365
## [2,] 1.1515 1.5341
## [3,] 1.0408 1.1749
##
## $`No. of sig LD terms`
## [1] 0
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 4440.175 5223.739 4104.771
##
## $Time
## user system elapsed
## 245.86 0.17 246.39
summary(m1, what = 'qlambda')## 1 2 3
## I1 0.7267 0.0000 0.0000
## I2 0.7174 0.0000 0.0000
## I3 0.7347 0.0000 0.0000
## I4 0.7412 0.0000 0.0000
## I5 0.7332 0.2608 0.0000
## I6 0.7001 0.2541 0.0000
## I7 0.0000 0.7281 0.0000
## I8 0.0000 0.7390 0.0000
## I9 0.0000 0.7309 0.0000
## I10 0.0000 0.7084 0.0000
## I11 0.0000 0.7163 0.2296
## I12 0.0000 0.7058 0.2424
## I13 0.0000 0.0000 0.7384
## I14 0.0000 0.0000 0.7249
## I15 0.0000 0.0000 0.7290
## I16 0.0000 0.0000 0.7118
## I17 0.2468 0.0000 0.7328
## I18 0.2735 0.0000 0.6678
summary(m1, what = 'offpsx') #summarize significant LD terms## row col est sd lower upper sig
summary(m1,what='eigen')## est sd lower upper sig
## F1 3.4084 0.4528 2.5969 4.3290 1
## F2 3.3473 0.3250 2.7404 4.0345 1
## F3 3.3178 0.4089 2.5469 4.1735 1
summary(m1,what='thd')## [,1] [,2] [,3]
## [1,] -1.3459 0.0683 1.6090
## [2,] -1.4491 0.0559 1.4960
## [3,] -1.4544 0.0525 1.4999
## [4,] -1.3818 0.0531 1.5951
## [5,] -1.4195 0.0143 1.4589
## [6,] -1.4877 0.0794 1.5676
## [7,] -1.4933 0.0406 1.6500
## [8,] -1.5286 -0.0571 1.4116
## [9,] -1.4567 -0.0098 1.4929
## [10,] -1.4996 0.0126 1.6338
## [11,] -1.4561 0.0223 1.5706
## [12,] -1.5264 0.0201 1.6214
## [13,] -1.5780 -0.0639 1.3885
## [14,] -1.4250 0.0390 1.4975
## [15,] -1.5565 -0.0362 1.4656
## [16,] -1.4636 -0.0190 1.3684
## [17,] -1.4411 0.0505 1.4726
## [18,] -1.5269 0.0258 1.5274
#plotting factorial eigenvalue
plot_lawbl(m1) # trace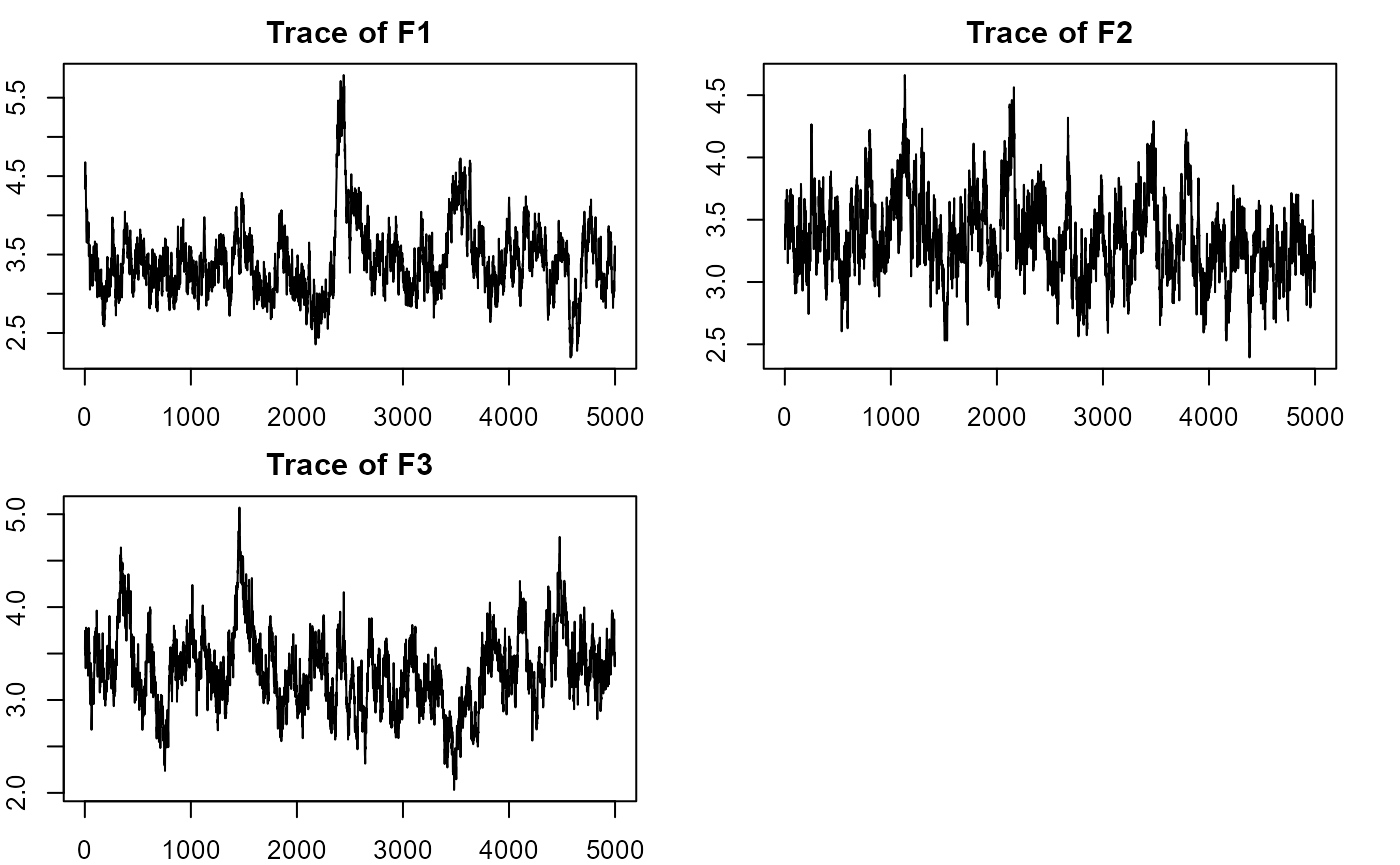
plot_lawbl(m1, what='density') #density
plot_lawbl(m1, what='EPSR') #EPSR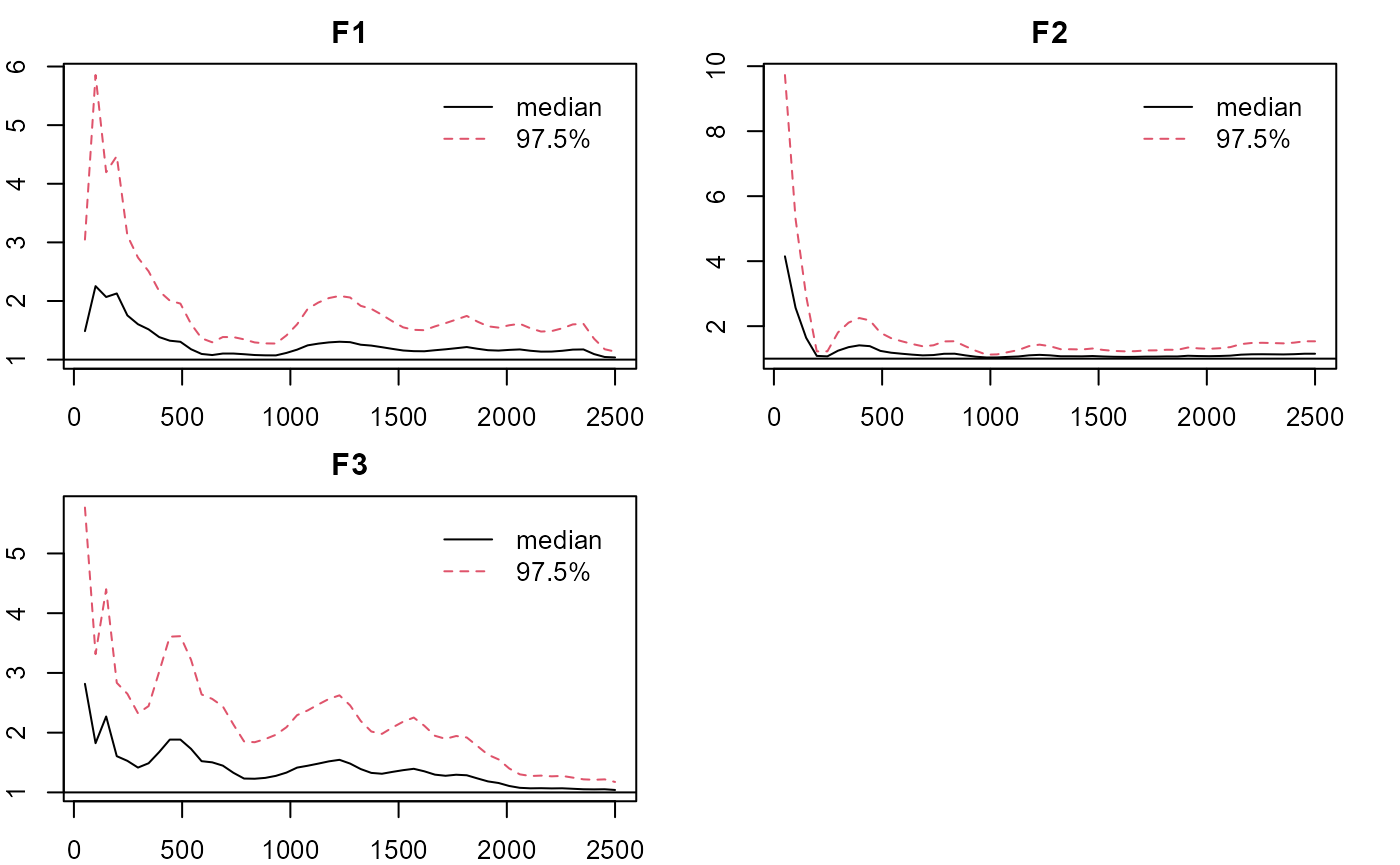
- CFA-LD: One can also configure the Q matrix for a CCFA model with local dependence (i.e. without any unspecified loading) based on results from the C-step.
Q<-summary(m1, what="qlambda")
Q[Q!=0]<-1
Q## 1 2 3
## I1 1 0 0
## I2 1 0 0
## I3 1 0 0
## I4 1 0 0
## I5 1 1 0
## I6 1 1 0
## I7 0 1 0
## I8 0 1 0
## I9 0 1 0
## I10 0 1 0
## I11 0 1 1
## I12 0 1 1
## I13 0 0 1
## I14 0 0 1
## I15 0 0 1
## I16 0 0 1
## I17 1 0 1
## I18 1 0 1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 9.888889
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0076 1.0164
## [2,] 1.0308 1.1020
## [3,] 1.0186 1.0865
##
## $`No. of sig LD terms`
## [1] 0
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 4247.119 4696.680 3724.944
##
## $Time
## user system elapsed
## 214.17 0.15 214.51
summary(m2, what = 'qlambda') ## 1 2 3
## I1 0.7056 0.0000 0.0000
## I2 0.7227 0.0000 0.0000
## I3 0.6963 0.0000 0.0000
## I4 0.7289 0.0000 0.0000
## I5 0.7036 0.3015 0.0000
## I6 0.6923 0.3032 0.0000
## I7 0.0000 0.6828 0.0000
## I8 0.0000 0.7527 0.0000
## I9 0.0000 0.6927 0.0000
## I10 0.0000 0.6862 0.0000
## I11 0.0000 0.6785 0.3011
## I12 0.0000 0.6968 0.3375
## I13 0.0000 0.0000 0.7063
## I14 0.0000 0.0000 0.7253
## I15 0.0000 0.0000 0.6930
## I16 0.0000 0.0000 0.7205
## I17 0.2925 0.0000 0.6826
## I18 0.3184 0.0000 0.6644
summary(m2, what = 'offpsx')## row col est sd lower upper sig
summary(m2,what='eigen')## est sd lower upper sig
## F1 3.2121 0.1904 2.8286 3.5794 1
## F2 3.1286 0.1873 2.7798 3.5067 1
## F3 3.1529 0.1942 2.7775 3.5456 1
summary(m2,what='thd')## [,1] [,2] [,3]
## [1,] -1.3475 0.0734 1.6202
## [2,] -1.4352 0.0640 1.5033
## [3,] -1.4400 0.0575 1.5008
## [4,] -1.3773 0.0622 1.6034
## [5,] -1.4175 0.0229 1.4704
## [6,] -1.4756 0.0891 1.5653
## [7,] -1.4872 0.0434 1.6372
## [8,] -1.5166 -0.0560 1.4114
## [9,] -1.4524 -0.0072 1.4929
## [10,] -1.4758 0.0154 1.6270
## [11,] -1.4475 0.0272 1.5720
## [12,] -1.5205 0.0250 1.6386
## [13,] -1.5645 -0.0583 1.3987
## [14,] -1.4151 0.0478 1.5086
## [15,] -1.5323 -0.0250 1.4645
## [16,] -1.4516 -0.0098 1.3737
## [17,] -1.4297 0.0592 1.4922
## [18,] -1.5078 0.0364 1.5444
plot_lawbl(m2) # Eigens' traces are excellent without regularization of the loadings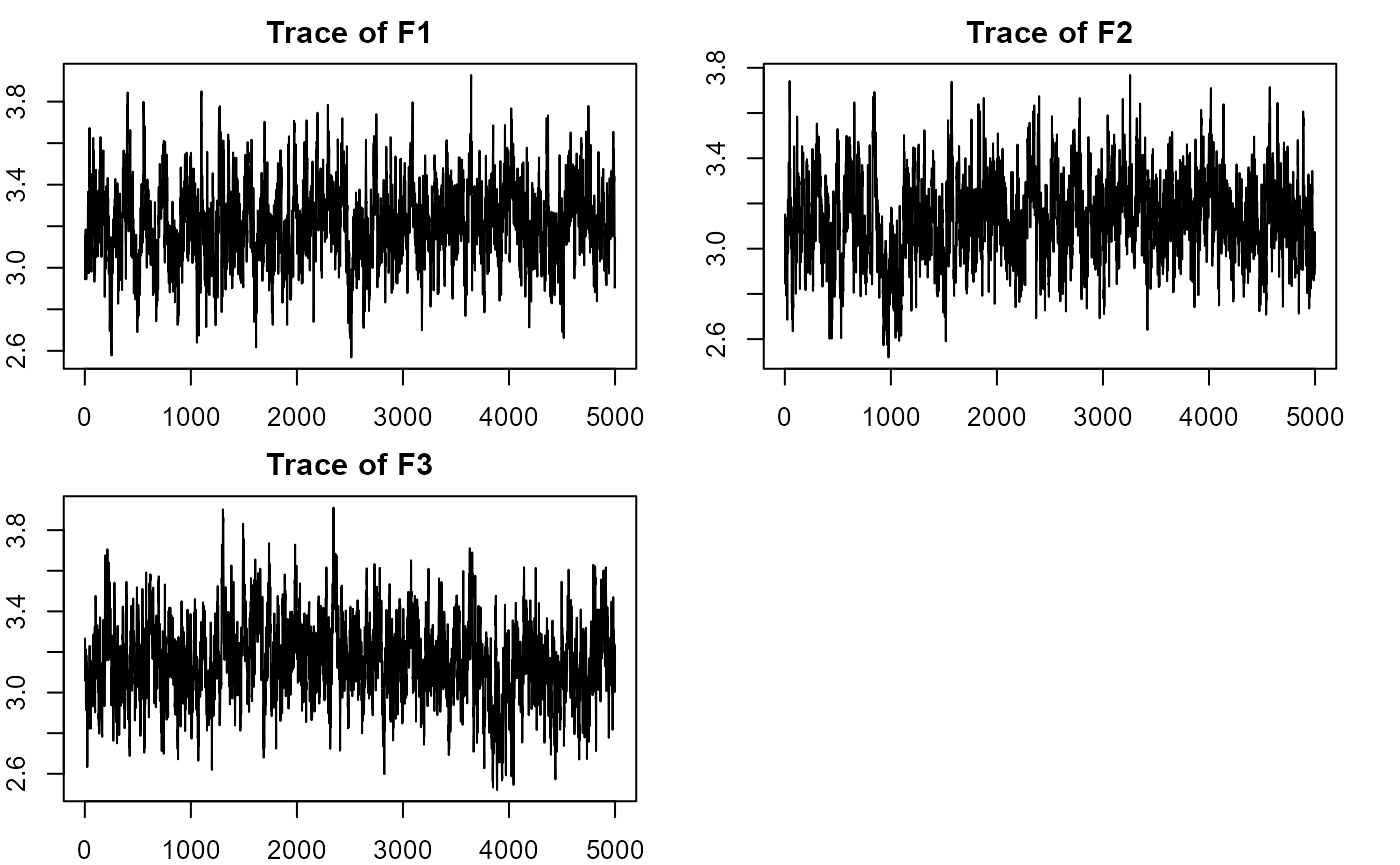
Categorical Data with Missingness and Local Dependence:
- Obtain the data and check the true loading pattern (qlam) and local dependence.
dat <- sim18ccfa41$dat
summary(dat) #10% missingness at random## V1 V2 V3 V4
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :2.000 Median :2.000
## Mean :2.505 Mean :2.497 Mean :2.496 Mean :2.506
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :84 NA's :101 NA's :104 NA's :95
## V5 V6 V7 V8 V9
## Min. :1.000 Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.00 1st Qu.:2.000 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :2.00 Median :3.000 Median :2.000
## Mean :2.524 Mean :2.515 Mean :2.49 Mean :2.532 Mean :2.499
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.00 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.00 Max. :4.000 Max. :4.000
## NA's :84 NA's :104 NA's :85 NA's :94 NA's :112
## V10 V11 V12 V13 V14
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.0 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.0 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :3.000 Median :3.0 Median :3.000
## Mean :2.514 Mean :2.503 Mean :2.502 Mean :2.5 Mean :2.503
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.0 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.0 Max. :4.000
## NA's :125 NA's :105 NA's :96 NA's :118 NA's :86
## V15 V16 V17 V18
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.00
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.00
## Median :3.000 Median :3.000 Median :3.000 Median :3.00
## Mean :2.528 Mean :2.515 Mean :2.503 Mean :2.53
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.00
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.00
## NA's :116 NA's :89 NA's :120 NA's :110
J <- ncol(dat) # no. of items
K <- 3 # no. of factors
sim18ccfa41$qlam## [,1] [,2] [,3]
## [1,] 0.7 0.0 0.0
## [2,] 0.7 0.0 0.0
## [3,] 0.7 0.0 0.0
## [4,] 0.7 0.0 0.0
## [5,] 0.7 0.3 0.0
## [6,] 0.7 0.3 0.0
## [7,] 0.0 0.7 0.0
## [8,] 0.0 0.7 0.0
## [9,] 0.0 0.7 0.0
## [10,] 0.0 0.7 0.0
## [11,] 0.0 0.7 0.3
## [12,] 0.0 0.7 0.3
## [13,] 0.0 0.0 0.7
## [14,] 0.0 0.0 0.7
## [15,] 0.0 0.0 0.7
## [16,] 0.0 0.0 0.7
## [17,] 0.3 0.0 0.7
## [18,] 0.3 0.0 0.7
sim18ccfa41$LD # effect size = .3## row col
## [1,] 14 1
## [2,] 7 2
## [3,] 4 3
## [4,] 13 8
## [5,] 10 9
## [6,] 16 15- E-step: Estimate with the GPCFA-LI model (E-step) by setting LD=FALSE and the design matrix Q. Only a few loadings need to be specified in Q (e.g., 2 per factor). Some loading estimates are biased due to ignoring the LD. So do the eigenvalues.
Q<-matrix(-1,J,K); # -1 for unspecified items
Q[1:2,1]<-Q[7:8,2]<-Q[13:14,3]<-1 # 1 for specified items
Q## [,1] [,2] [,3]
## [1,] 1 -1 -1
## [2,] 1 -1 -1
## [3,] -1 -1 -1
## [4,] -1 -1 -1
## [5,] -1 -1 -1
## [6,] -1 -1 -1
## [7,] -1 1 -1
## [8,] -1 1 -1
## [9,] -1 -1 -1
## [10,] -1 -1 -1
## [11,] -1 -1 -1
## [12,] -1 -1 -1
## [13,] -1 -1 1
## [14,] -1 -1 1
## [15,] -1 -1 -1
## [16,] -1 -1 -1
## [17,] -1 -1 -1
## [18,] -1 -1 -1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] FALSE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 23
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.4580 2.3875
## [2,] 1.9994 4.0405
## [3,] 1.1967 1.6815
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 3738.775 3687.415 3319.333
##
## $Time
## user system elapsed
## 171.36 0.05 171.63
summary(m0, what = 'qlambda')## 1 2 3
## I1 0.6543 0.0000 0.0000
## I2 0.7263 0.0000 0.0000
## I3 0.8019 0.0000 0.0000
## I4 0.7970 0.0000 0.0000
## I5 0.6798 0.2779 0.0000
## I6 0.6462 0.2727 0.0000
## I7 0.0000 0.6286 0.0000
## I8 0.0000 0.6336 0.0000
## I9 0.0000 0.8457 0.0000
## I10 0.0000 0.8292 0.0000
## I11 0.0000 0.6029 0.4254
## I12 0.0000 0.6159 0.3702
## I13 0.0000 0.0000 0.7052
## I14 0.0000 0.0000 0.7438
## I15 0.0000 0.0000 0.8766
## I16 0.0000 0.0000 0.8670
## I17 0.2373 0.0000 0.6922
## I18 0.0000 0.0000 0.7353
summary(m0,what='eigen')## est sd lower upper sig
## F1 3.3932 0.4361 2.5928 4.2149 1
## F2 3.3538 0.5630 2.3584 4.4203 1
## F3 4.0893 0.8231 2.8673 5.9234 1
summary(m0,what='thd')## [,1] [,2] [,3]
## [1,] -1.5197 -0.0118 1.5217
## [2,] -1.4287 -0.0156 1.5713
## [3,] -1.5167 0.0334 1.5375
## [4,] -1.6291 0.0278 1.5202
## [5,] -1.5382 -0.0372 1.4742
## [6,] -1.5829 -0.0201 1.5531
## [7,] -1.4971 -0.0116 1.5614
## [8,] -1.5561 -0.0513 1.4267
## [9,] -1.5959 -0.0135 1.5820
## [10,] -1.6099 -0.0289 1.5185
## [11,] -1.4588 -0.0442 1.4681
## [12,] -1.4584 -0.0653 1.5872
## [13,] -1.4944 -0.0075 1.5651
## [14,] -1.3893 -0.0212 1.4638
## [15,] -1.4857 -0.0390 1.4791
## [16,] -1.5244 -0.0167 1.4658
## [17,] -1.5263 -0.0132 1.5450
## [18,] -1.4941 -0.0327 1.4575
plot_lawbl(m0) # trace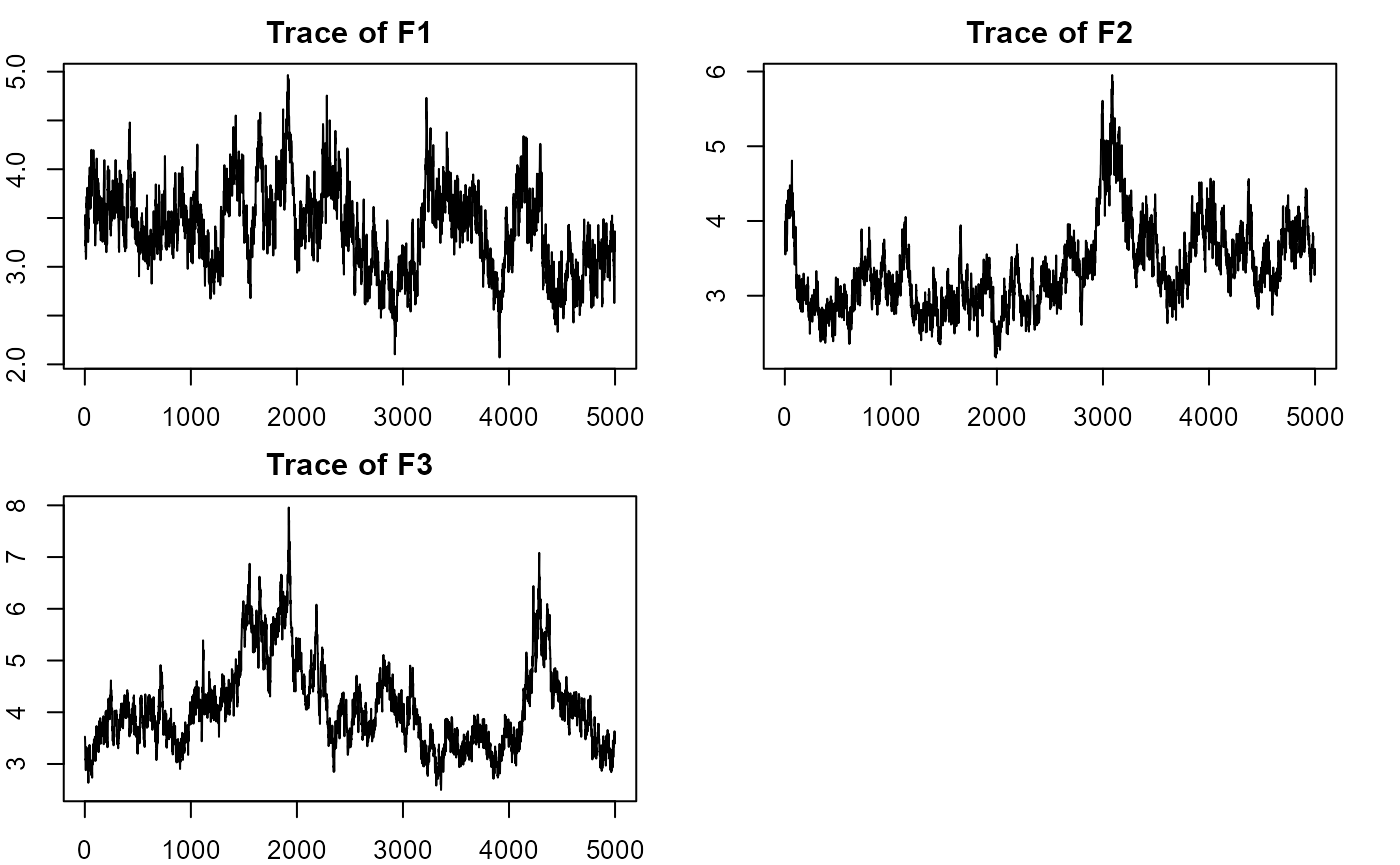
plot_lawbl(m0, what='EPSR') #EPSR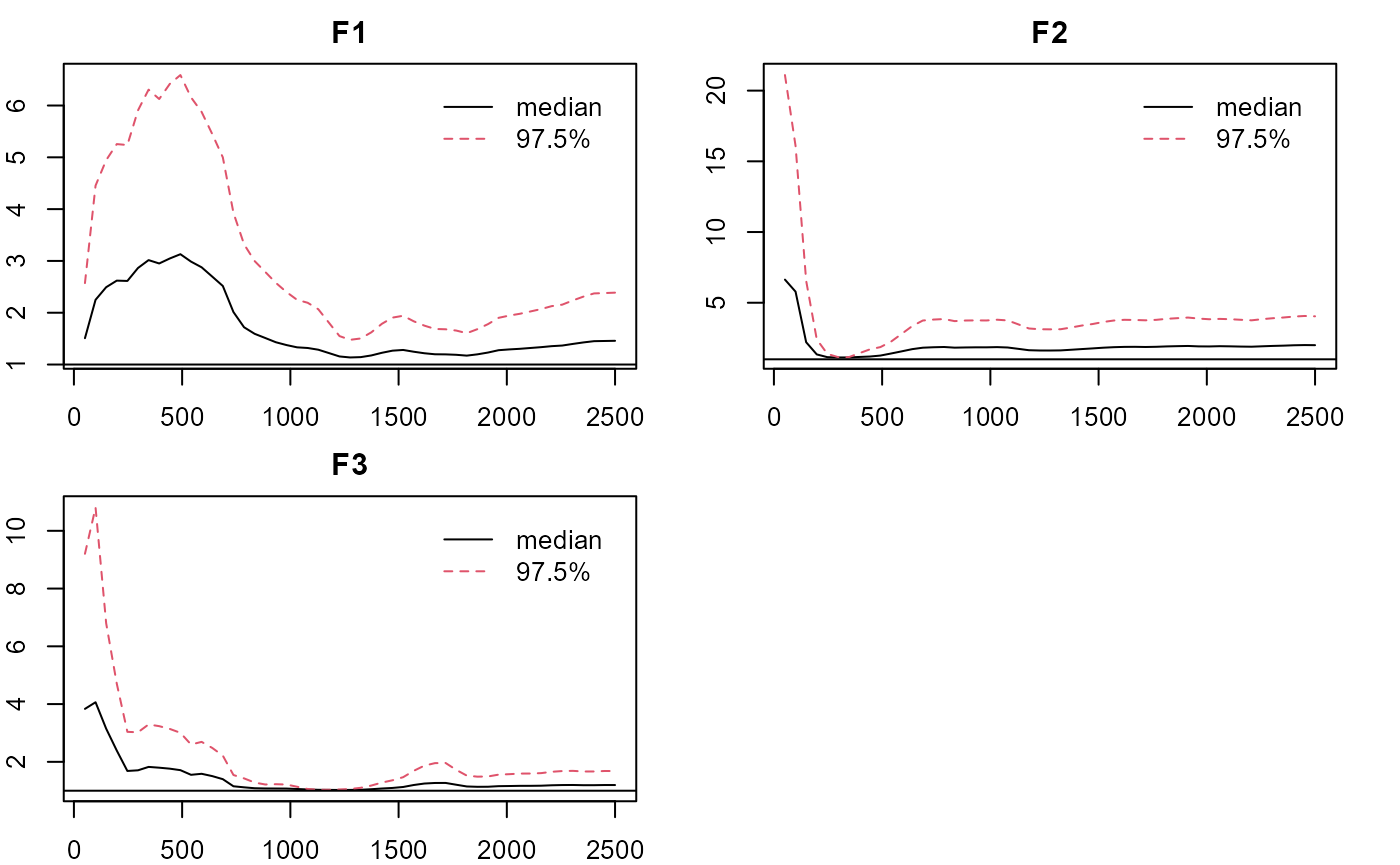
- C-step: Reconfigure the Q matrix for the C-step with one specified loading per item based on results from the E-step. Estimate with the GPCFA model by setting LD=TRUE (by default). The estimates are more accurate, and the LD terms can be largely recovered.
Q<-matrix(-1,J,K);
tmp<-summary(m0, what="qlambda")
cind<-apply(tmp,1,which.max)
Q[cbind(c(1:J),cind)]<-1
Q## [,1] [,2] [,3]
## [1,] 1 -1 -1
## [2,] 1 -1 -1
## [3,] 1 -1 -1
## [4,] 1 -1 -1
## [5,] 1 -1 -1
## [6,] 1 -1 -1
## [7,] -1 1 -1
## [8,] -1 1 -1
## [9,] -1 1 -1
## [10,] -1 1 -1
## [11,] -1 1 -1
## [12,] -1 1 -1
## [13,] -1 -1 1
## [14,] -1 -1 1
## [15,] -1 -1 1
## [16,] -1 -1 1
## [17,] -1 -1 1
## [18,] -1 -1 1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0606 1.2375
## [2,] 1.1442 1.5127
## [3,] 1.0213 1.0360
##
## $`No. of sig LD terms`
## [1] 6
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 4056.808 4814.414 3695.445
##
## $Time
## user system elapsed
## 239.00 0.08 239.35
summary(m1, what = 'qlambda')## 1 2 3
## I1 0.7013 0.0000 0.0000
## I2 0.7248 0.0000 0.0000
## I3 0.7387 0.0000 0.0000
## I4 0.7439 0.0000 0.0000
## I5 0.7146 0.2324 0.0000
## I6 0.6920 0.2382 0.0000
## I7 0.0000 0.6955 0.0000
## I8 0.0000 0.6794 0.0000
## I9 0.0000 0.7872 0.0000
## I10 0.0000 0.7624 0.0000
## I11 0.0000 0.6771 0.3361
## I12 0.0000 0.7016 0.2786
## I13 0.0000 0.0000 0.6898
## I14 0.0000 0.0000 0.7249
## I15 0.0000 0.0000 0.7834
## I16 0.0000 0.0000 0.7671
## I17 0.2378 0.0000 0.6904
## I18 0.1815 0.0000 0.7180
summary(m1,what='eigen')## est sd lower upper sig
## F1 3.2874 0.3379 2.7130 4.0566 1
## F2 3.3166 0.3758 2.5306 4.0954 1
## F3 3.5054 0.3906 2.7670 4.2822 1
summary(m1, what = 'offpsx')## row col est sd lower upper sig
## [1,] 14 1 0.2298 0.0485 0.1373 0.3297 1
## [2,] 7 2 0.1967 0.0461 0.1072 0.2883 1
## [3,] 4 3 0.1916 0.0649 0.0840 0.3414 1
## [4,] 13 8 0.2002 0.0417 0.1191 0.2837 1
## [5,] 10 9 0.1939 0.0705 0.0583 0.3293 1
## [6,] 16 15 0.1890 0.0743 0.0462 0.3248 1
summary(m1,what='thd')## [,1] [,2] [,3]
## [1,] -1.5481 -0.0169 1.5362
## [2,] -1.4707 -0.0202 1.5870
## [3,] -1.5306 0.0274 1.5410
## [4,] -1.6467 0.0209 1.5355
## [5,] -1.5333 -0.0363 1.4573
## [6,] -1.5638 -0.0219 1.5392
## [7,] -1.5129 -0.0077 1.5872
## [8,] -1.5810 -0.0442 1.4556
## [9,] -1.6115 -0.0061 1.6081
## [10,] -1.6479 -0.0212 1.5501
## [11,] -1.4545 -0.0385 1.4659
## [12,] -1.4504 -0.0612 1.5905
## [13,] -1.5193 -0.0064 1.5701
## [14,] -1.4234 -0.0249 1.4884
## [15,] -1.5135 -0.0521 1.4970
## [16,] -1.5519 -0.0201 1.4865
## [17,] -1.5281 -0.0204 1.5393
## [18,] -1.4973 -0.0386 1.4489- CFA-LD: Configure the Q matrix for a CCFA model with local dependence (i.e. without any unspecified loading) based on results from the C-step. Results are better than, but similar to the C-step.
Q<-summary(m1, what="qlambda")
Q[Q!=0]<-1
Q## 1 2 3
## I1 1 0 0
## I2 1 0 0
## I3 1 0 0
## I4 1 0 0
## I5 1 1 0
## I6 1 1 0
## I7 0 1 0
## I8 0 1 0
## I9 0 1 0
## I10 0 1 0
## I11 0 1 1
## I12 0 1 1
## I13 0 0 1
## I14 0 0 1
## I15 0 0 1
## I16 0 0 1
## I17 1 0 1
## I18 1 0 1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 0.9999 1.0004
## [2,] 1.0226 1.0925
## [3,] 1.0118 1.0118
##
## $`No. of sig LD terms`
## [1] 6
##
## $`Cat Items`
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 3837.865 4053.762 3082.027
##
## $Time
## user system elapsed
## 220.89 0.12 221.38
summary(m2, what = 'qlambda') ## 1 2 3
## I1 0.6868 0.0000 0.0000
## I2 0.7149 0.0000 0.0000
## I3 0.7259 0.0000 0.0000
## I4 0.7261 0.0000 0.0000
## I5 0.7030 0.2744 0.0000
## I6 0.6775 0.2868 0.0000
## I7 0.0000 0.6958 0.0000
## I8 0.0000 0.7012 0.0000
## I9 0.0000 0.7566 0.0000
## I10 0.0000 0.7550 0.0000
## I11 0.0000 0.6467 0.3948
## I12 0.0000 0.6724 0.3567
## I13 0.0000 0.0000 0.6934
## I14 0.0000 0.0000 0.6984
## I15 0.0000 0.0000 0.7650
## I16 0.0000 0.0000 0.7498
## I17 0.3187 0.0000 0.6888
## I18 0.2408 0.0000 0.7205
summary(m2,what='eigen')## est sd lower upper sig
## F1 3.1686 0.2157 2.7597 3.6062 1
## F2 3.1622 0.1865 2.8028 3.5308 1
## F3 3.4081 0.2017 3.0128 3.8007 1
summary(m2, what = 'offpsx')## row col est sd lower upper sig
## [1,] 14 1 0.2662 0.0362 0.1935 0.3354 1
## [2,] 7 2 0.2279 0.0368 0.1591 0.3017 1
## [3,] 4 3 0.1939 0.0606 0.0811 0.3107 1
## [4,] 13 8 0.2173 0.0359 0.1471 0.2862 1
## [5,] 10 9 0.1768 0.0493 0.0838 0.2780 1
## [6,] 16 15 0.1958 0.0500 0.0965 0.2906 1
summary(m2,what='thd')## [,1] [,2] [,3]
## [1,] -1.5487 -0.0057 1.5504
## [2,] -1.4580 -0.0111 1.6059
## [3,] -1.5197 0.0359 1.5563
## [4,] -1.6426 0.0321 1.5525
## [5,] -1.5292 -0.0240 1.4794
## [6,] -1.5455 -0.0083 1.5423
## [7,] -1.5052 -0.0044 1.5769
## [8,] -1.5690 -0.0423 1.4425
## [9,] -1.6117 -0.0013 1.6046
## [10,] -1.6249 -0.0165 1.5503
## [11,] -1.4469 -0.0312 1.4732
## [12,] -1.4453 -0.0542 1.6037
## [13,] -1.5088 -0.0040 1.5699
## [14,] -1.4217 -0.0207 1.5002
## [15,] -1.4990 -0.0420 1.5054
## [16,] -1.5506 -0.0140 1.4988
## [17,] -1.5112 -0.0103 1.5572
## [18,] -1.4811 -0.0254 1.4605Mixed-type Data with Missingness and Local Dependence:
- Obtain the data and check the true loading pattern (qlam) and local dependence.
dat <- sim18mcfa41$dat
summary(dat) #10% missingness at random## V1 V2 V3 V4
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :2.000 Median :2.000
## Mean :2.505 Mean :2.497 Mean :2.496 Mean :2.506
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
## NA's :84 NA's :101 NA's :104 NA's :95
## V5 V6 V7 V8
## Min. :1.000 Min. :1.000 Min. :-2.81026 Min. :-3.23753
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:-0.71029 1st Qu.:-0.62884
## Median :3.000 Median :3.000 Median :-0.00391 Median : 0.04407
## Mean :2.524 Mean :2.515 Mean :-0.01609 Mean : 0.05464
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.: 0.64606 3rd Qu.: 0.76442
## Max. :4.000 Max. :4.000 Max. : 2.70247 Max. : 2.89557
## NA's :84 NA's :104 NA's :85 NA's :94
## V9 V10 V11 V12
## Min. :-3.30561 Min. :-3.02592 Min. :-3.41374 Min. :-2.82342
## 1st Qu.:-0.66089 1st Qu.:-0.61385 1st Qu.:-0.63676 1st Qu.:-0.67127
## Median :-0.00165 Median : 0.01598 Median : 0.01521 Median : 0.04094
## Mean : 0.00834 Mean : 0.02074 Mean : 0.00846 Mean : 0.01327
## 3rd Qu.: 0.68991 3rd Qu.: 0.69146 3rd Qu.: 0.70011 3rd Qu.: 0.69313
## Max. : 3.29942 Max. : 3.03966 Max. : 3.24879 Max. : 3.37976
## NA's :112 NA's :125 NA's :105 NA's :96
## V13 V14 V15 V16
## Min. :-2.91486 Min. :-3.35077 Min. :-3.79077 Min. :-2.98539
## 1st Qu.:-0.63790 1st Qu.:-0.68802 1st Qu.:-0.59432 1st Qu.:-0.65737
## Median : 0.01362 Median : 0.04734 Median : 0.07327 Median : 0.03254
## Mean : 0.01722 Mean : 0.00211 Mean : 0.04284 Mean : 0.01089
## 3rd Qu.: 0.69528 3rd Qu.: 0.67515 3rd Qu.: 0.73561 3rd Qu.: 0.69205
## Max. : 3.44561 Max. : 2.93371 Max. : 3.35474 Max. : 3.16500
## NA's :118 NA's :86 NA's :116 NA's :89
## V17 V18
## Min. :-2.72783 Min. :-2.98409
## 1st Qu.:-0.64767 1st Qu.:-0.68150
## Median : 0.02905 Median : 0.06052
## Mean : 0.00466 Mean : 0.03421
## 3rd Qu.: 0.63216 3rd Qu.: 0.71505
## Max. : 3.28462 Max. : 3.06039
## NA's :120 NA's :110
J <- ncol(dat) # no. of items
K <- 3 # no. of factors
sim18mcfa41$qlam## [,1] [,2] [,3]
## [1,] 0.7 0.0 0.0
## [2,] 0.7 0.0 0.0
## [3,] 0.7 0.0 0.0
## [4,] 0.7 0.0 0.0
## [5,] 0.7 0.3 0.0
## [6,] 0.7 0.3 0.0
## [7,] 0.0 0.7 0.0
## [8,] 0.0 0.7 0.0
## [9,] 0.0 0.7 0.0
## [10,] 0.0 0.7 0.0
## [11,] 0.0 0.7 0.3
## [12,] 0.0 0.7 0.3
## [13,] 0.0 0.0 0.7
## [14,] 0.0 0.0 0.7
## [15,] 0.0 0.0 0.7
## [16,] 0.0 0.0 0.7
## [17,] 0.3 0.0 0.7
## [18,] 0.3 0.0 0.7
sim18mcfa41$LD # effect size = .3## row col
## [1,] 14 1
## [2,] 7 2
## [3,] 4 3
## [4,] 13 8
## [5,] 10 9
## [6,] 16 15- E-step: Estimate with the GPCFA-LI model (E-step) by setting LD=FALSE and the design matrix Q. Only a few loadings need to be specified in Q (e.g., 2 per factor). The first 6 items are categorical and need to be specified with cati.
Q<-matrix(-1,J,K); # -1 for unspecified items
Q[1:2,1]<-Q[7:8,2]<-Q[13:14,3]<-1 # 1 for specified items
Q## [,1] [,2] [,3]
## [1,] 1 -1 -1
## [2,] 1 -1 -1
## [3,] -1 -1 -1
## [4,] -1 -1 -1
## [5,] -1 -1 -1
## [6,] -1 -1 -1
## [7,] -1 1 -1
## [8,] -1 1 -1
## [9,] -1 -1 -1
## [10,] -1 -1 -1
## [11,] -1 -1 -1
## [12,] -1 -1 -1
## [13,] -1 -1 1
## [14,] -1 -1 1
## [15,] -1 -1 -1
## [16,] -1 -1 -1
## [17,] -1 -1 -1
## [18,] -1 -1 -1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] FALSE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.1481 1.4378
## [2,] 1.0588 1.2261
## [3,] 1.0571 1.1682
##
## $`Cat Items`
## [1] 1 2 3 4 5 6
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 3875.109 2565.383 2197.301
##
## $Time
## user system elapsed
## 98.39 0.03 98.45
summary(m0, what = 'qlambda')## 1 2 3
## I1 0.6876 0.0000 0.0000
## I2 0.7572 0.0000 0.0000
## I3 0.8128 0.0000 0.0000
## I4 0.8082 0.0000 0.0000
## I5 0.6787 0.2801 0.0000
## I6 0.6383 0.2853 0.0000
## I7 0.0000 0.6618 0.0000
## I8 0.0000 0.6822 0.0000
## I9 0.0000 0.8713 0.0000
## I10 0.0000 0.8685 0.0000
## I11 0.0000 0.6839 0.2978
## I12 0.0000 0.6821 0.2826
## I13 0.0000 0.0000 0.6637
## I14 0.0000 0.0000 0.6640
## I15 0.0000 0.0000 0.8562
## I16 0.0000 0.0000 0.8737
## I17 0.2816 0.0000 0.6517
## I18 0.2267 0.0000 0.6745
summary(m0,what='eigen')## est sd lower upper sig
## F1 3.5173 0.5809 2.6630 4.6969 1
## F2 3.6563 0.5120 2.7873 4.7220 1
## F3 3.5761 0.4549 2.7268 4.4855 1
summary(m0,what='thd') # only for 12 items ## [,1] [,2] [,3]
## [1,] -1.5116 -0.0136 1.5195
## [2,] -1.4373 -0.0177 1.5803
## [3,] -1.5156 0.0281 1.5275
## [4,] -1.6250 0.0245 1.5176
## [5,] -1.5312 -0.0392 1.4713
## [6,] -1.5594 -0.0179 1.5400
plot_lawbl(m0) # trace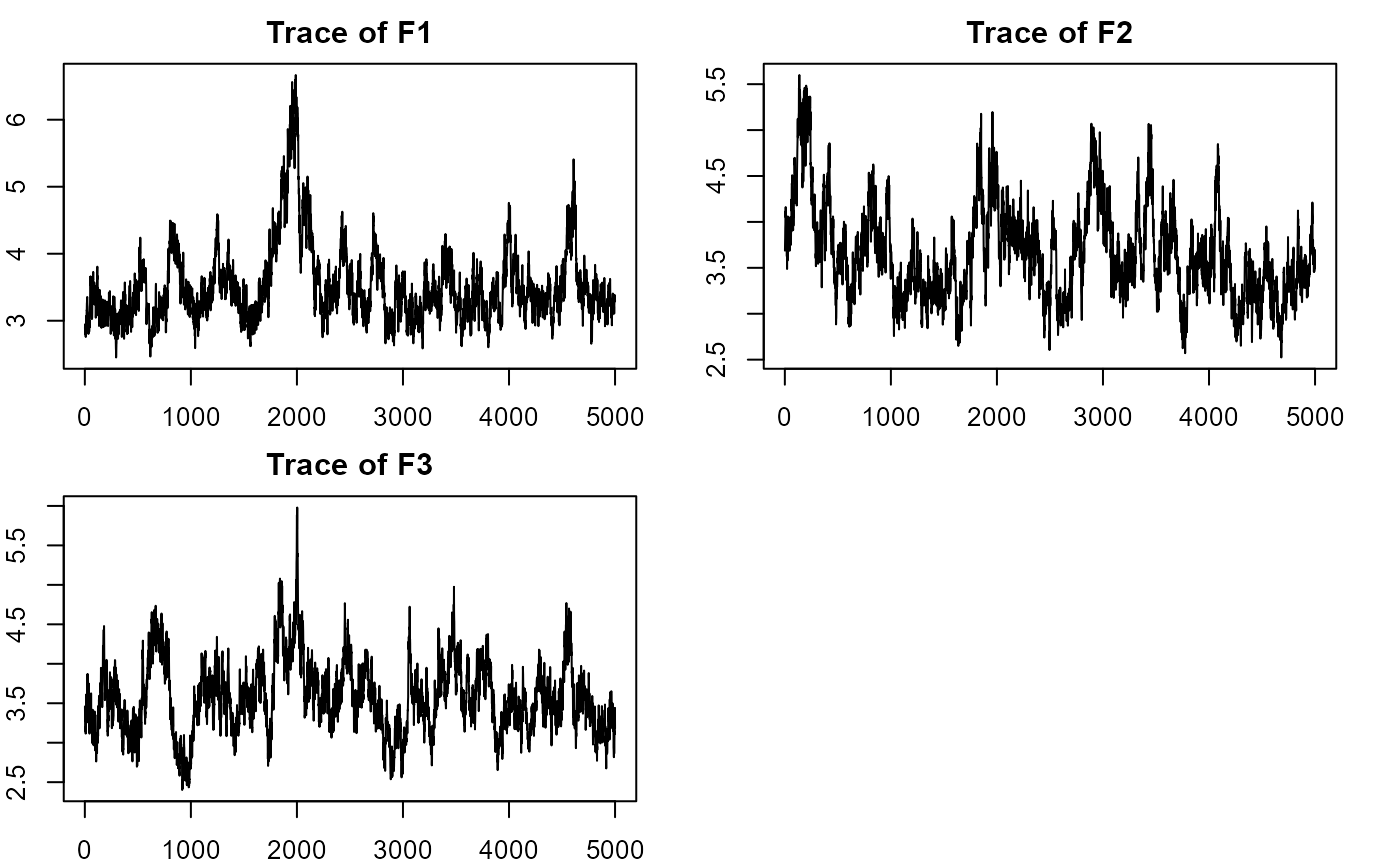
plot_lawbl(m0, what='density')
plot_lawbl(m0, what='EPSR') #EPSR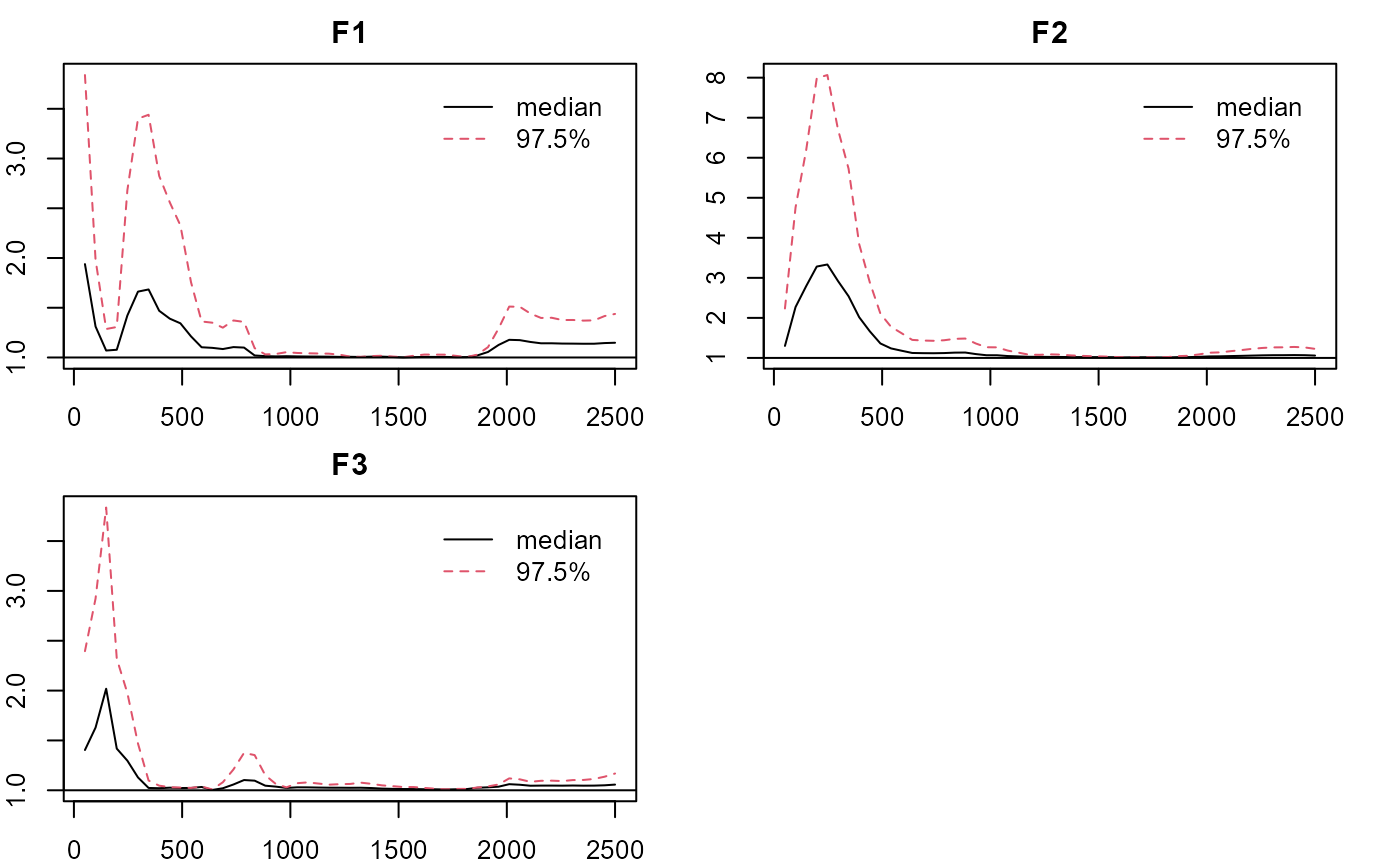
- C-step: Reconfigure the Q matrix for the C-step with one specified loading per item based on results from the E-step. Estimate with the GPCFA model by setting LD=TRUE (by default). The estimates are more accurate, and the LD terms can be largely recovered.
Q<-matrix(-1,J,K);
tmp<-summary(m0, what="qlambda")
cind<-apply(tmp,1,which.max)
Q[cbind(c(1:J),cind)]<-1
Q## [,1] [,2] [,3]
## [1,] 1 -1 -1
## [2,] 1 -1 -1
## [3,] 1 -1 -1
## [4,] 1 -1 -1
## [5,] 1 -1 -1
## [6,] 1 -1 -1
## [7,] -1 1 -1
## [8,] -1 1 -1
## [9,] -1 1 -1
## [10,] -1 1 -1
## [11,] -1 1 -1
## [12,] -1 1 -1
## [13,] -1 -1 1
## [14,] -1 -1 1
## [15,] -1 -1 1
## [16,] -1 -1 1
## [17,] -1 -1 1
## [18,] -1 -1 1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0014 1.0018
## [2,] 1.0160 1.0737
## [3,] 1.0069 1.0344
##
## $`No. of sig LD terms`
## [1] 6
##
## $`Cat Items`
## [1] 1 2 3 4 5 6
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 3598.992 3455.159 2336.191
##
## $Time
## user system elapsed
## 166.89 0.08 167.24
summary(m1, what = 'qlambda')## 1 2 3
## I1 0.7066 0.0000 0.0000
## I2 0.7088 0.0000 0.0000
## I3 0.7555 0.0000 0.0000
## I4 0.7599 0.0000 0.0000
## I5 0.7038 0.2372 0.0000
## I6 0.6854 0.2493 0.0000
## I7 0.0000 0.6944 0.0000
## I8 0.0000 0.6916 0.0000
## I9 0.0000 0.7420 0.0000
## I10 0.0000 0.7357 0.0000
## I11 0.0000 0.6813 0.3079
## I12 0.0000 0.7045 0.2768
## I13 0.0000 0.0000 0.7112
## I14 0.0000 0.0000 0.6745
## I15 0.0000 0.0000 0.7393
## I16 0.0000 0.0000 0.7509
## I17 0.2593 0.0000 0.6897
## I18 0.2022 0.0000 0.7185
summary(m1,what='eigen')## est sd lower upper sig
## F1 3.3038 0.2860 2.7999 3.8838 1
## F2 3.2225 0.2984 2.6530 3.8015 1
## F3 3.3168 0.3385 2.6656 3.9809 1
summary(m1, what = 'offpsx')## row col est sd lower upper sig
## [1,] 14 1 0.2651 0.0455 0.1782 0.3575 1
## [2,] 7 2 0.2406 0.0501 0.1383 0.3371 1
## [3,] 4 3 0.1705 0.0655 0.0378 0.2954 1
## [4,] 13 8 0.2391 0.0419 0.1626 0.3244 1
## [5,] 10 9 0.2517 0.0612 0.1305 0.3687 1
## [6,] 16 15 0.2387 0.0568 0.1218 0.3378 1
summary(m1,what='thd')## [,1] [,2] [,3]
## [1,] -1.5341 -0.0186 1.5166
## [2,] -1.4704 -0.0244 1.5781
## [3,] -1.5264 0.0223 1.5391
## [4,] -1.6330 0.0191 1.5240
## [5,] -1.5267 -0.0365 1.4651
## [6,] -1.5480 -0.0243 1.5299- CFA-LD: Configure the Q matrix for a mix of CFA and CCFA model with local dependence (i.e. without any unspecified loading) based on results from the C-step. Results are better than, but similar to the C-step.
Q<-summary(m1, what="qlambda")
Q[Q!=0]<-1
Q## 1 2 3
## I1 1 0 0
## I2 1 0 0
## I3 1 0 0
## I4 1 0 0
## I5 1 1 0
## I6 1 1 0
## I7 0 1 0
## I8 0 1 0
## I9 0 1 0
## I10 0 1 0
## I11 0 1 1
## I12 0 1 1
## I13 0 0 1
## I14 0 0 1
## I15 0 0 1
## I16 0 0 1
## I17 1 0 1
## I18 1 0 1## $NJK
## [1] 1000 18 3
##
## $`Miss%`
## [1] 10.15556
##
## $`LD Allowed`
## [1] TRUE
##
## $`Burn in`
## [1] 5000
##
## $Iteration
## [1] 5000
##
## $`No. of sig lambda`
## [1] 24
##
## $Selected
## [1] TRUE TRUE TRUE
##
## $`Auto, NCONV, MCONV`
## [1] 0 0 10
##
## $EPSR
## Point est. Upper C.I.
## [1,] 1.0129 1.0174
## [2,] 1.0100 1.0438
## [3,] 1.0181 1.0578
##
## $`No. of sig LD terms`
## [1] 6
##
## $`Cat Items`
## [1] 1 2 3 4 5 6
##
## $`max No. of categories`
## [1] 4
##
## $`DIC, BIC, AIC`
## [1] 3316.863 2617.938 1646.202
##
## $Time
## user system elapsed
## 141.18 0.06 141.41
summary(m2, what = 'qlambda') ## 1 2 3
## I1 0.6837 0.0000 0.0000
## I2 0.7024 0.0000 0.0000
## I3 0.7379 0.0000 0.0000
## I4 0.7342 0.0000 0.0000
## I5 0.6921 0.2838 0.0000
## I6 0.6792 0.2919 0.0000
## I7 0.0000 0.6970 0.0000
## I8 0.0000 0.7018 0.0000
## I9 0.0000 0.7336 0.0000
## I10 0.0000 0.7529 0.0000
## I11 0.0000 0.6666 0.3383
## I12 0.0000 0.6929 0.3096
## I13 0.0000 0.0000 0.7030
## I14 0.0000 0.0000 0.6693
## I15 0.0000 0.0000 0.7628
## I16 0.0000 0.0000 0.7660
## I17 0.3063 0.0000 0.6879
## I18 0.2502 0.0000 0.7082
summary(m2,what='eigen')## est sd lower upper sig
## F1 3.1570 0.1883 2.7964 3.5213 1
## F2 3.1866 0.1807 2.8363 3.5337 1
## F3 3.3083 0.1863 2.9527 3.6702 1
summary(m2, what = 'offpsx')## row col est sd lower upper sig
## [1,] 14 1 0.2931 0.0347 0.2264 0.3607 1
## [2,] 7 2 0.2774 0.0321 0.2166 0.3424 1
## [3,] 4 3 0.1791 0.0543 0.0649 0.2770 1
## [4,] 13 8 0.2508 0.0307 0.1943 0.3160 1
## [5,] 10 9 0.2330 0.0505 0.1378 0.3277 1
## [6,] 16 15 0.2114 0.0488 0.1181 0.3022 1
summary(m2,what='thd')## [,1] [,2] [,3]
## [1,] -1.5324 -0.0136 1.5230
## [2,] -1.4692 -0.0213 1.5880
## [3,] -1.5265 0.0306 1.5477
## [4,] -1.6268 0.0222 1.5286
## [5,] -1.5233 -0.0347 1.4636
## [6,] -1.5557 -0.0227 1.5423