Note: the estimation process can be time consuming depending on the computing power. You can same some time by reducing the length of the chains.
Continuous Data w/o Local Dependence:
- Load the package, obtain the data, loading pattern (qlam), and setup the design matrix Q.
library(LAWBL)
dat <- sim18cfa0$dat
J <- ncol(dat) # no. of items
K <- 3 # no. of factors
qlam <- sim18cfa0$qlam
qlam
R> [,1] [,2] [,3]
R> [1,] 0.7 0.0 0.0
R> [2,] 0.7 0.0 0.0
R> [3,] 0.7 0.0 0.0
R> [4,] 0.7 0.0 0.0
R> [5,] 0.7 0.3 0.0
R> [6,] 0.7 0.3 0.0
R> [7,] 0.0 0.7 0.0
R> [8,] 0.0 0.7 0.0
R> [9,] 0.0 0.7 0.0
R> [10,] 0.0 0.7 0.0
R> [11,] 0.0 0.7 0.3
R> [12,] 0.0 0.7 0.3
R> [13,] 0.0 0.0 0.7
R> [14,] 0.0 0.0 0.7
R> [15,] 0.0 0.0 0.7
R> [16,] 0.0 0.0 0.7
R> [17,] 0.3 0.0 0.7
R> [18,] 0.3 0.0 0.7
Q<-matrix(-1,J,K); # -1 for unspecified items
Q[1:2,1]<-Q[7:8,2]<-Q[13:14,3]<-1 # 1 for specified items
Q
R> [,1] [,2] [,3]
R> [1,] 1 -1 -1
R> [2,] 1 -1 -1
R> [3,] -1 -1 -1
R> [4,] -1 -1 -1
R> [5,] -1 -1 -1
R> [6,] -1 -1 -1
R> [7,] -1 1 -1
R> [8,] -1 1 -1
R> [9,] -1 -1 -1
R> [10,] -1 -1 -1
R> [11,] -1 -1 -1
R> [12,] -1 -1 -1
R> [13,] -1 -1 1
R> [14,] -1 -1 1
R> [15,] -1 -1 -1
R> [16,] -1 -1 -1
R> [17,] -1 -1 -1
R> [18,] -1 -1 -1- E-step: Estimate with the PCFA-LI model (E-step) by setting LD=F. Only a few loadings need to be specified in Q (e.g., 2 per factor). Longer chain is suggested for stabler performance (burn=iter=5,000 by default).
m0 <- pcfa(dat = dat, Q = Q,LD = FALSE, burn = 2000, iter = 2000,verbose = TRUE)
R>
R> Tot. Iter = 1000
R> [,1] [,2] [,3]
R> Feigen 4.027 3.873 2.503
R> NLA_lg3 8.000 6.000 6.000
R> Shrink 3.219 3.219 3.219
R>
R> Tot. Iter = 2000
R> [,1] [,2] [,3]
R> Feigen 3.626 3.688 4.227
R> NLA_lg3 6.000 6.000 6.000
R> Shrink 2.705 2.705 2.705
R>
R> Tot. Iter = 3000
R> [,1] [,2] [,3]
R> Feigen 3.757 3.545 4.346
R> NLA_lg3 6.000 6.000 7.000
R> Shrink 3.614 3.614 3.614
R> Adj PSR 1.092 1.809 1.729
R>
R> Tot. Iter = 4000
R> [,1] [,2] [,3]
R> Feigen 2.677 3.699 3.423
R> NLA_lg3 6.000 6.000 7.000
R> Shrink 3.153 3.153 3.153
R> Adj PSR 1.001 1.006 1.021
R>
R> #Sign change: 0 0 0 0 0 0
R> user system elapsed
R> 16.53 0.02 16.56
# summarize basic information
summary(m0)
R> $N
R> [1] 1000
R>
R> $J
R> [1] 18
R>
R> $K
R> [1] 3
R>
R> $`Miss%`
R> [1] 0
R>
R> $`LD enabled`
R> [1] FALSE
R>
R> $`Burn in`
R> [1] 2000
R>
R> $Iteration
R> [1] 2000
R>
R> $`No. of sig lambda`
R> [1] 24
R>
R> $`Adj. PSR`
R> Point est. Upper C.I.
R> F1 1.000692 1.000992
R> F2 1.006334 1.030777
R> F3 1.020804 1.022674
#summarize significant loadings in pattern/Q-matrix format
summary(m0, what = 'qlambda')
R> [,1] [,2] [,3]
R> I1 0.6881938 0.0000000 0.0000000
R> I2 0.7276617 0.0000000 0.0000000
R> I3 0.7053776 0.0000000 0.0000000
R> I4 0.6525335 0.0000000 0.0000000
R> I5 0.7120300 0.2865062 0.0000000
R> I6 0.7095454 0.2982842 0.0000000
R> I7 0.0000000 0.7413281 0.0000000
R> I8 0.0000000 0.7388007 0.0000000
R> I9 0.0000000 0.7328911 0.0000000
R> I10 0.0000000 0.6653911 0.0000000
R> I11 0.0000000 0.7037540 0.2547656
R> I12 0.0000000 0.7147327 0.2628362
R> I13 0.0000000 0.0000000 0.7521188
R> I14 0.0000000 0.0000000 0.7831557
R> I15 0.0000000 0.0000000 0.7695287
R> I16 0.0000000 0.0000000 0.7263737
R> I17 0.2407217 0.0000000 0.7269717
R> I18 0.2450948 0.0000000 0.7290218
#factorial eigenvalue
summary(m0,what='eigen')
R> est sd lower upper sig
R> F1 3.157885 0.5277766 2.128743 4.166953 1
R> F2 3.387151 0.4077793 2.640005 4.243836 1
R> F3 3.600655 0.4920634 2.666980 4.561343 1
#plotting factorial eigenvalue
plot_eigen(m0) # trace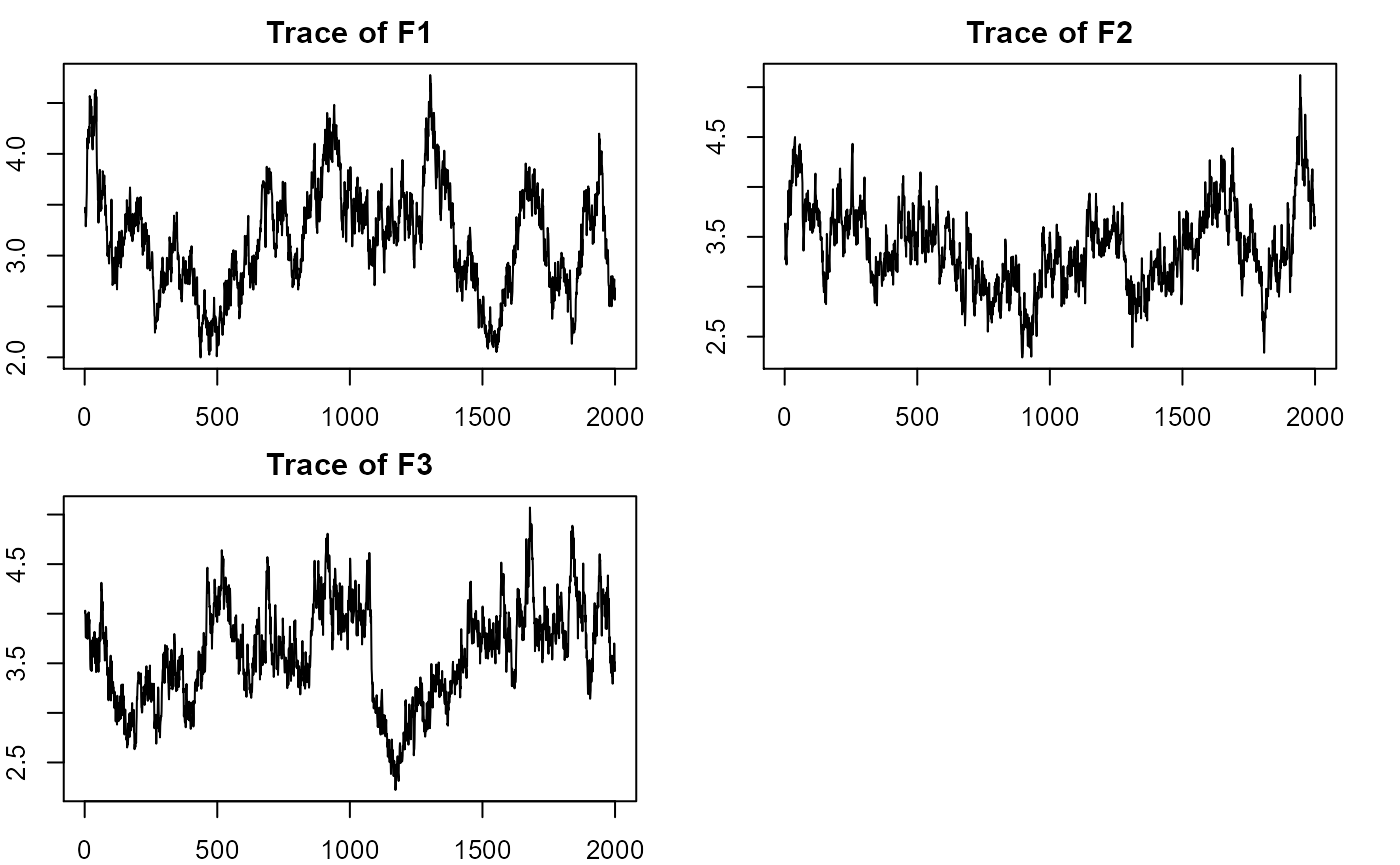
plot_eigen(m0, what='density') #density

plot_eigen(m0, what='APSR') #adj, PSRF
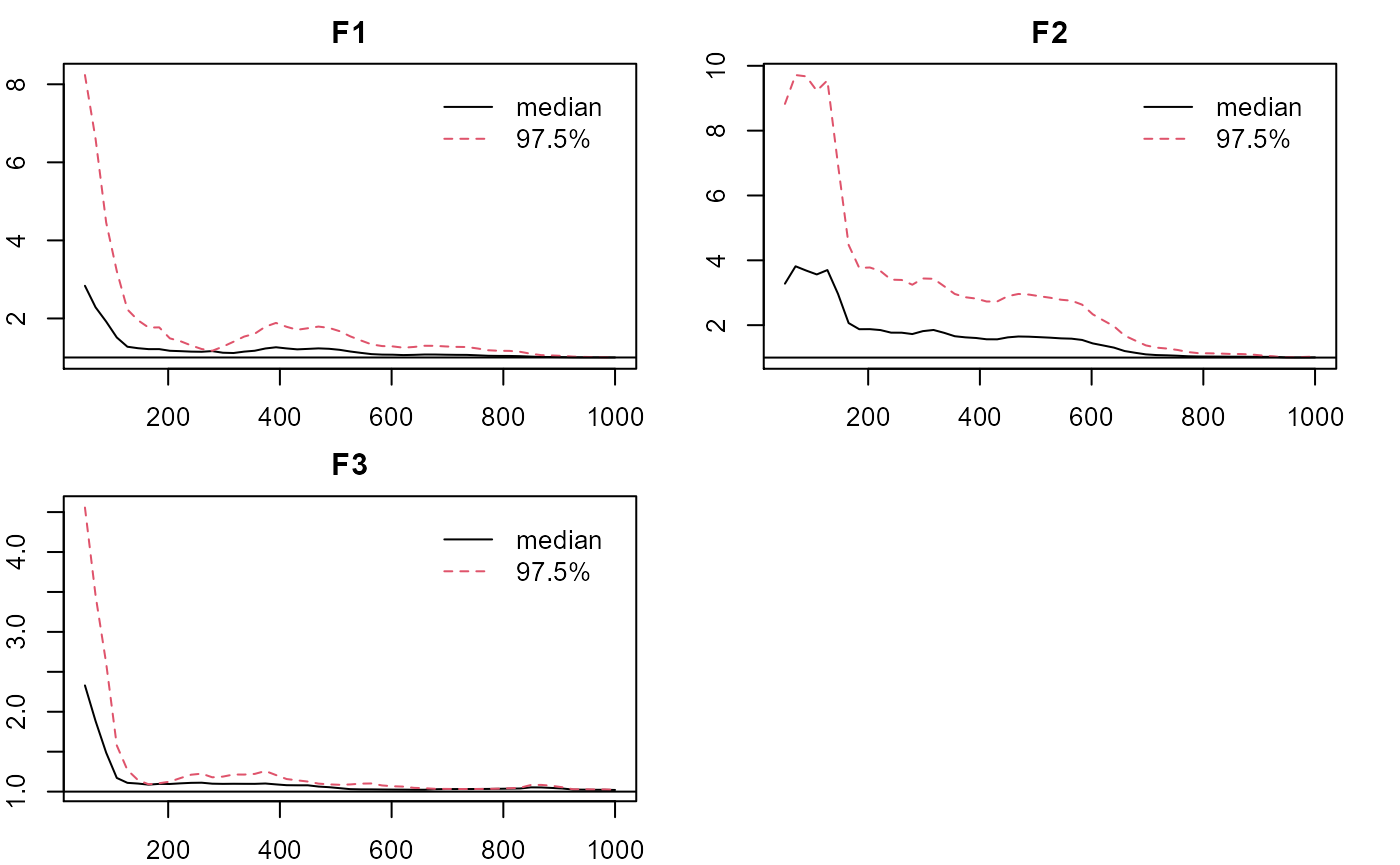
- C-step: Reconfigure the Q matrix for the C-step with one specified loading per item based on results from the E-step. Estimate with the PCFA model by setting LD=TRUE (by default). Longer chain is suggested for stabler performance. Results are very close to the E-step, since there’s no LD in the data.
Q<-matrix(-1,J,K); tmp<-summary(m0, what="qlambda") cind<-apply(tmp,1,which.max) Q[cbind(c(1:J),cind)]<-1 #alternatively #Q[1:6,1]<-Q[7:12,2]<-Q[13:18,3]<-1 # 1 for specified items m1 <- pcfa(dat = dat, Q = Q, burn = 2000, iter = 2000,verbose = TRUE) summary(m1) summary(m1, what = 'qlambda') summary(m1, what = 'offpsx') #summarize significant LD terms summary(m1,what='eigen') #plotting factorial eigenvalue # par(mar = rep(2, 4)) plot_eigen(m1) # trace plot_eigen(m1, what='density') #density plot_eigen(m1, what='APSR') #adj, PSRF
- CFA-LD: One can also configure the Q matrix for a CFA model with local dependence (i.e. without any unspecified loading) based on results from the C-step. Results are also very close.
Continuous Data with Local Dependence:
- Load the the data, loading pattern (qlam), and LD terms, and setup the design matrix Q.
dat <- sim18cfa1$dat J <- ncol(dat) # no. of items K <- 3 # no. of factors sim18cfa1$qlam sim18cfa1$LD # effect size = .3 Q<-matrix(-1,J,K); # -1 for unspecified items Q[1:2,1]<-Q[7:8,2]<-Q[13:14,3]<-1 # 1 for specified items Q
- E-step: Estimate with the PCFA-LI model (E-step) by setting LD=FALSE. Only a few loadings need to be specified in Q (e.g., 2 per factor). Some loading estimates are biased due to ignoring the LD. So do the eigenvalues.
m0 <- pcfa(dat = dat, Q = Q,LD = FALSE, burn = 4000, iter = 4000,verbose = TRUE) summary(m0) summary(m0, what = 'qlambda') summary(m0,what='eigen') plot_eigen(m0) # trace plot_eigen(m0, what='APSR')
- C-step: Reconfigure the Q matrix for the C-step with one specified loading per item based on results from the E-step. Estimate with the PCFA model by setting LD=TRUE (by default). The estimates are more accurate, and the LD terms can be largely recovered.
Q<-matrix(-1,J,K); tmp<-summary(m0, what="qlambda") cind<-apply(tmp,1,which.max) Q[cbind(c(1:J),cind)]<-1 Q m1 <- pcfa(dat = dat, Q = Q,burn = 4000, iter = 4000,verbose = TRUE) summary(m1) summary(m1, what = 'qlambda') summary(m1,what='eigen') summary(m1, what = 'offpsx')
- CFA-LD: Configure the Q matrix for a CFA model with local dependence (i.e. without any unspecified loading) based on results from the C-step. Results are better than, but similar to the C-step.